What Is Mode What Is Median In Math

Mean Mode Median

Mean, median, and fashion are the iii measures of fundamental trend in statistics. Nosotros identify the central position of whatever data gear up while describing a set up of data. This is known as the mensurate of central tendency. We come beyond data every day. We find them in newspapers, articles, in our bank statements, mobile and electricity bills. The listing is endless; they are present all around usa. Now the question arises if we can figure out some important features of the information by considering only certain representatives of the data. This is possible by using measures of cardinal tendency or averages, namely hateful, median, and mode.

Allow usa empathise hateful, median, and mode in item in the following sections using solved examples.

one.	Mean, Median, and Mode in Statistics
2.	Mean
3.	Median
4.	Fashion
v.	Mean, Median, and Mode Formulas
half-dozen.	Relation between Hateful, Median, and Mode
vii.	Divergence between Mean and Boilerplate
8.	Difference betwixt Mean and Median
9.	FAQs on Hateful, Median, and Mode

Mean, Median and Mode in Statistics

Hateful, median, and style are the measures of central tendency, used to study the various characteristics of a given fix of data. A measure out of central trend describes a set of data by identifying the primal position in the data set up equally a single value. We tin can think of information technology as a tendency of data to cluster effectually a middle value. In statistics, the three most mutual measures of fundamental tendencies are Hateful, Median, and Manner. Choosing the best measure of fundamental trend depends on the blazon of information we accept.

Let'south brainstorm by understanding the meaning of each of these terms.

Mean

The arithmetics mean of a given information is the sum of all observations divided past the number of observations. For example, a cricketer's scores in five ODI matches are as follows: 12, 34, 45, fifty, 24. To find his average score in a match, we calculate the arithmetic hateful of data using the mean formula:

Mean = Sum of all observations/Number of observations

Mean = (12 + 34 + 45 + 50 + 24)/5

Hateful = 165/5 = 33

Hateful is denoted past x̄ (pronounced equally x bar).

Types of Data

Data can be nowadays in raw form or tabular form. Let's discover the hateful in both cases.

Raw Information

Let ten_one, x_ii, x₃ , . . . , ten_n be n observations.

We can find the arithmetic mean using the mean formula.

Mean, x̄ = (ten₁+ ten₂+ ... + 10_n)/north

Example: If the heights of v people are 142 cm, 150 cm, 149 cm, 156 cm, and 153 cm.

Find the mean height.

Mean height, x̄ = (142 + 150 + 149 + 156 + 153)/five
= 750/5
= 150

Hateful, x̄ = 150 cm

Thus, the mean acme is 150 cm.

Frequency Distribution (Tabular) Class

When the data is present in tabular form, we use the following formula:

Hateful, x̄ = (x_if₁ + x_twof₂+ ... + x_nf_n)/(f_ane+ f₂+ ... + f_n)

Consider the following case.

Example i: Find the mean of the post-obit distribution:

x	iv	6	9	10	15
f	5	10	10	7	8

Solution:

Calculation table for arithmetics hateful:

10i	fi	xifi
4	five	20
6	10	60
9	10	90
x	7	70
15	8	120
	∑ fi= 40	∑ xi fi= 360

Mean, x̄ = (∑x_if_i)/(∑f_i)
= 360/twoscore
= 9

Thus, Mean = 9

Instance two: Hither is an example where the information is in the form of form intervals. The following table indicates the data on the number of patients visiting a infirmary in a calendar month. Find the boilerplate number of patients visiting the hospital in a solar day.

Number of patients	Number of days visiting hospital
0-x	2
ten-twenty	6
20-30	nine
30-forty	vii
40-50	4
l-threescore	2

Solution:

In this case, we find the classmark (also called as mid-indicate of a form) for each class.

Note: Form marker = (lower limit + upper limit)/2

Let x₁, x_two, x₃ , . . . , x_north be the course marks of the respective classes.

Hence, we get the following table:

Class mark (xi)	frequency (fi)	xifi
5	2	x
15	6	90
25	9	225
35	7	245
45	iv	180
55	2	110
Total	∑ fi= thirty	∑ fixi= 860

Mean, x̄ = (∑ x_if_i)/(∑ f_i)
= 860/30
= 28.67

x̄ = 28.67

Challenging Question:

Permit the mean of x_ane, x₂, x_iii … 10_n be A, then what is the hateful of:

• (x₁ + k), (ten_two + k), (x₃ + k), … , (x_{due north} + thousand)
• (x_one - k), (x₂ - k), (x_three - k), … , (x_n - k)
• kx_ane, kx₂, kx_iii, … , kx_n

Median

The value of the middlemost ascertainment, obtained afterward arranging the data in ascending or descending lodge, is chosen the median of the data.

For example, consider the data: 4, four, vi, 3, 2. Allow's arrange this data in ascending gild: 2, 3, 4, four, 6. In that location are v observations. Thus, median = centre value i.e. 4.

Case ane: Ungrouped Data

• Step 1: Arrange the data in ascending or descending order.
• Step 2: Let the total number of observations exist n.

To find the median, we need to consider if n is fifty-fifty or odd. If n is odd, then use the formula:

Median = (n + 1)/2^th ascertainment

Example 1: Let's consider the data: 56, 67, 54, 34, 78, 43, 23. What is the median?

Solution:

Arranging in ascending lodge, we get: 23, 34, 43, 54, 56, 67, 78. Here, n (number of observations) = 7

So, (7 + i)/2 = 4

∴ Median = 4^th observation

Median = 54

If n is fifty-fifty, then use the formula:

Median = [(n/2)^th obs.+ ((n/two) + 1)^th obs.]/two

Example ii: Let's consider the data: 50, 67, 24, 34, 78, 43. What is the median?

Solution:

Arranging in ascending order, we get: 24, 34, 43, 50, 67, 78.

Here, n (no.of observations) = six

half dozen/2 = iii

Using the median formula,

Median = (3^rd obs. + 4^th obs.)/2

= (43 + l)/2

Median = 46.five

Case 2: Grouped Information

When the data is continuous and in the course of a frequency distribution, the median is constitute every bit shown below:

Footstep 1: Find the median class.

Allow north = total number of observations i.east. ∑ f_i

Note: Median Class is the class where (n/2) lies.

Step 2: Use the following formula to find the median.

Median = \( l + [\dfrac {\dfrac{due north}{ii}-c}{f}]\times h\)

where,

• fifty = lower limit of median grade
• c = cumulative frequency of the class preceding the median class
• f = frequency of the median class
• h = class size

Let's consider the post-obit example to understand this amend.

Example: Find the median marks for the post-obit distribution:

Classes	0-x	10-20	20-30	xxx-40	40-50
Frequency	ii	12	22	8	6

Solution:

We need to calculate the cumulative frequencies to find the median.

Calculation tabular array:

Classes	Number of students	Cumulative frequency
0-10	2	2
10-20	12	2 + 12 = xiv
20-30	22	fourteen + 22 = 36
thirty-xl	8	36 + 8 = 44
40-fifty	6	44 + 6 = fifty

N = 50

North/ii = fifty/2 = 25

Median Class = (20 - 30)

l = 20, f = 22, c = 14, h = x

Using Median formula:

Median = \(fifty + [\dfrac {\dfrac{n}{2}-c}{f}]\times h\)

= 20 + (25 - 14)/22 × 10

= 20 + (11/22) × 10

= 20 + v = 25

∴ Median = 25

Manner

The value which appears near oft in the given data i.e. the observation with the highest frequency is called a style of data.

Case 1: Ungrouped Data

For ungrouped information, we just demand to identify the observation which occurs maximum times.

Fashion = Observation with maximum frequency

For example in the information: 6, 8, nine, 3, 4, 6, 7, half dozen, 3, the value 6 appears the most number of times. Thus, mode = 6. An easy way to remember mode is: Most Often Data Eastwardntered. Note: A information may have no mode, 1 mode, or more than 1 fashion. Depending upon the number of modes the information has, it tin can be chosen unimodal, bimodal, trimodal, or multimodal.

The example discussed above has only 1 manner, and so it is unimodal.

Case 2: Grouped Data

When the information is continuous, the manner tin be found using the following steps:

• Stride 1: Observe modal grade i.e. the form with maximum frequency.
• Step ii: Notice fashion using the following formula:

Manner = \(fifty + [\dfrac {f_m-f_1}{2f_m-f_1-f_2}]\times h\)

where,

• l = lower limit of modal class,
• f_thousand = frequency of modal form,
• f₁= frequency of course preceding modal class,
• f₂= frequency of grade succeeding modal form,
• h = grade width

Consider the following example to understand the formula.

Example: Observe the mode of the given data:

Marks Obtained	0-20	20-twoscore	xl-60	60-80	lxxx-100
Number of students	5	10	12	6	three

Solution:

The highest frequency = 12, and then the modal class is forty-60.

fifty = lower limit of modal class = 40

f_g = frequency of modal class = 12

f₁ = frequency of grade preceding modal grade = x

f_ii = frequency of class succeeding modal class = 6

h = class width = 20

Using the mode formula,

Mode = \(l + [\dfrac {f_m-f_1}{2f_m-f_1-f_2}]\times h\)

= forty + \([\dfrac{12-x}{2 \times 12 - 10-half-dozen} ]\times 20\)

= xl + (2/8) × xx

= 45

∴ Mode = 45

Mean, Median and Fashion Formulas

Nosotros covered the formulas and method to detect the hateful, median, and mode for grouped and ungrouped gear up of data. Let us summarize and recall them using the listing of mean, median, and mode formulas given below,

Mean formula for ungrouped data: Sum of all observations/Number of observations

Hateful formula for grouped data: x̄ = (x₁f₁ + x_twof_two+ ... + x_{due north}f_north)/(f_one+ f₂+ ... + f_n)

Median formula for ungrouped data: If north is odd, so employ the formula: Median = (n + 1)/2^thursday observation. If n is even, and then use the formula: Median = [(northward/2)^th obs.+ ((northward/2) + 1)^th obs.]/ii

Median formula for grouped data: Median = \( l + [\dfrac {\dfrac{n}{2}-c}{f}]\times h\)

where,

• fifty = lower limit of median class
• c = cumulative frequency of the course preceding the median course
• f = frequency of the median grade
• h = class size

Mode formula for ungrouped data: Mode = Observation with maximum frequency

Mode formula for grouped information: Way = \(50 + [\dfrac {f_m-f_1}{2f_m-f_1-f_2}]\times h\)

where,

• l = lower limit of modal class,
• f_m = frequency of modal course,
• f₁ = frequency of form preceding modal class,
• f₂ = frequency of form succeeding modal form,
• h = class width

Relation Betwixt Mean, Median and Mode

The three measures of primal values i.due east. hateful, median, and manner are closely connected past the following relations (called an empirical relationship).

2Mean + Manner = 3Median

For case, if we are asked to calculate the mean, median, and style of continuous grouped data, then we tin can calculate mean and median using the formulas as discussed in the previous sections and then discover style using the empirical relation.

For example, we take information whose fashion = 65 and median = 61.vi.

Then, nosotros tin can find the mean using the above mean, median, and mode relation.

2Mean + Mode = 3 Median

∴2Mean = iii × 61.6 - 65

∴2Mean = 119.viii

⇒ Mean = 119.8/2

⇒ Mean = 59.9

Difference Between Mean and Average

The term average is frequently used in everyday life to denote a value that is typical for a group of quantities. Boilerplate rainfall in a month or the average age of employees of an organization is a typical instance. We might read an article stating "People spend an average of 2 hours every day on social media. " Nosotros understand from the use of the term average that non anybody is spending 2 hours a mean solar day on social media just some spend more time and some less.

Even so, we tin can understand from the term boilerplate that 2 hours is a good indicator of the corporeality of time spent on social media per 24-hour interval. About people use average and mean interchangeably even though they are not the same.

• Boilerplate is the value that indicates what is near likely to be expected.
• They help to summarise large data into a single value.

An average tends to lie centrally with the values of the observations arranged in ascending gild of magnitude. And so, we call an boilerplate measure of the central tendency of the data. Averages are of different types. What nosotros refer to as mean i.e. the arithmetic hateful is one of the averages. Mean is called the mathematical average whereas median and mode are positional averages.

Departure Between Mean and Median

Mean is known every bit the mathematical average whereas the median is known as the positional boilerplate. To understand the deviation betwixt the two, consider the following example. A department of an organization has five employees which include a supervisor and four executives. The executives describe a salary of ₹x,000 per month while the supervisor gets ₹40,000.

Hateful = (10000 + 10000 + 10000 + 10000 + 40000)/5 = 80000/five = 16000

Thus, the mean salary is ₹16,000.

To discover the median, we consider the ascending order: 10000, 10000, 10000, 10000, 40000.

northward = 5,

so, (north + 1)/two = 3

Thus, the median is the 3rd observation.

Median = 10000

Thus, the median is ₹10,000 per month.

Now let us compare the two measures of central tendencies.

Nosotros can detect that the mean salary of ₹16,000 does not give even an estimated salary of any of the employees whereas the median salary represents the data more effectively.

I of the weaknesses of mean is that it gets affected past extreme values.

Await at the post-obit graph to empathize how extreme values touch on mean and median:

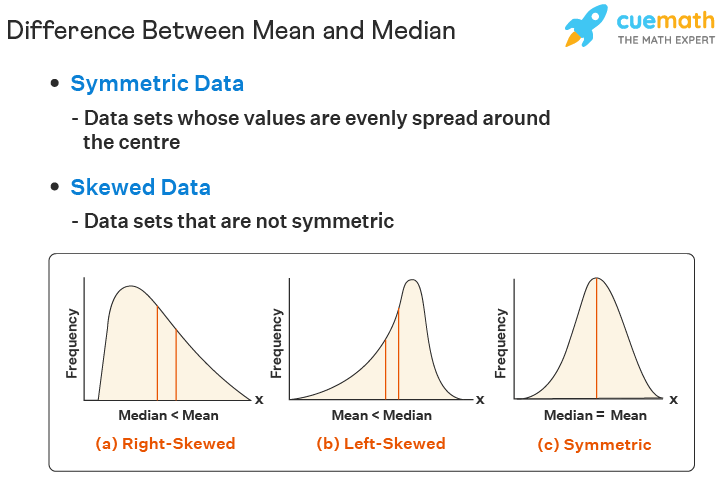
Then, mean is to be used when we don't have extremes in the data.

If nosotros have extreme points, then the median gives a better estimation.

Hither's a quick summary of the differences between the 2.

Mean Vs Median	Mean	Median
Definition	Average of given data (Mathematical Average)	The key value of information (Positional Boilerplate)
Calculation	Add all values and split up by the total number of observations	Arrange data in ascending / descending society and find the middle value
Values of information	Every value is considered for calculation	Every value is not considered
Result of extreme points	Profoundly afflicted by extreme points	Doesn't get affected past farthermost points

Related Topics on Mean, Median, and Mode:

• Boilerplate
• Categorical Data
• Range in Statistics
• Geometric Hateful

Solved Examples on Hateful, Median and Fashion

1. Example i: If the mean of the post-obit data is 20.six, observe the missing frequency (p).

   x	10	fifteen	20	25	35
   f	3	10	p	vii	5

   Solution:

   Let us make the calculation table for this :

   xi	fi	tenifi
   10	three	10 × 3 = 30
   xv	10	15 × 10 = 150
   20	p	20 × p = 20p
   25	7	25 × 7 = 175
   35	5	35 × 5 = 175
   Total:	∑ fi = 25 + p	∑ fi10i = 530 + 20p

   Mean = (∑ f_ix_i)/(∑ f_i)
   20.6 = (530 + 20p)/(25 + p)
   530 + 20p = 515 + xx.6p
   15 = 0.6p
   p =15/0.half-dozen
   = 25

   ∴ The missing frequency (p) = 25

2. Instance two: The mean of 5 numbers is 18. If one number is excluded, their mean is 16. Notice the excluded number.

   Solution:

   Given, north = 5, x̄ = eighteen

   x̄ = (∑x_i)/due north

   ∑ten_i= 5 × 18 = 90

   Thus, the full of 5 numbers = 90

   Let the excluded number be "a".

   Therefore, total of 4 numbers = 90 - a

   Hateful of four numbers = (90 - a)/4
   sixteen = (90 - a)/four
   90 - a = 64
   a = 26

   ⇒ The missing number is 26.

   1. Case 3: A survey on the heights (in cm) of 50 girls of grade Ten was conducted at a schoolhouse and the post-obit data were obtained:

      Height (in cm)	120-130	130-140	140-150	150-160	160-170	Total
      Number of girls	2	8	12	20	8	l

      Find the mode and median of the above data.

      Solution:

      Modal form = 150 - 160

      [as information technology has maximum frequency]

      l = 150, h = 10, f_{one thousand} = xx, f_i = 12, f₂ = 8

      Way = \(l + [\dfrac {f_m-f_1}{2f_m-f_1-f_2}]\times h\) = 150 + (20 - 12)/(ii × 20 - 12 - eight) × 10 = 150 + 4 = 154

      ∴ Fashion = 154

      To find the median, we need cumulative frequencies.

      Consider the table:

      Class Intervals	No. of girls (fi)	Cumulative frequency (c)
      120-130	2	2
      130-140	8	2 + 8 = 10
      140-150	12 = f1	10 + 12 = 22 (c)
      150-160	20 = fm	22 + 20 = 42
      160-170	8 = f2	42 + 8 = fifty (n)

      north = 50
      ⇒n/2 = 25

      ∴ Median course = (150 - 160)

      l = 150, c = 22, f = xx, h = 10

      Median = l + [(n/two - c)/f] × h = 150 + [((fifty/2) - 22)/20] × 10 = 150 + 1.v = 151.5

      ∴ Mode = 154, Median = 151.5

go to slidego to slidego to slide

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you sympathise the concepts through visualizations.

Book a Gratis Trial Course

Practise Questions on Mean, Median, Mode

get to slidego to slide

FAQs on Mean, Median, Mode

What is Mean, Median, Way in Statistics?

Mean, median, mode are measures of central trend or, in other words, different kinds of averages in statistics. Hateful is the "boilerplate", where we observe the full of all the numbers and so divide by the number of numbers, while the median is the "middle" value in the list of numbers. Mode is the value that occurs well-nigh frequently in the given ready of data.

What are Formulas to Find Mean, Median, and Mode?

Dissimilar sets of formulas tin be used to observe mean, median, and fashion depending upon the type of data if that is grouped or ungrouped. The following formulas can exist used to find the mean median and mode for ungrouped data:

• Hateful = Sum of all observations/Number of observations
• If n is odd, then utilize the formula: Median = (n + i)/2^th ascertainment. If north is even, then use the formula: Median = [(n/ii)^th obs.+ ((n/ii) + 1)^thursday obs.]/2
• Fashion = Observation with maximum frequency

How to Observe Mean, Median and Mode for Grouped Data?

We tin can detect the mean, manner, and median for grouped data using the below-given formulas,

Mean, x̄ = (x₁f_one + ten₂f₂+ ... + 10_nf_n)/( f₁+ f₂+ ... + f_n)

Median = \( l + [\dfrac {\dfrac{n}{two}-c}{f}]\times h\)
where,

• l = lower limit of median class
• c = cumulative frequency of the grade preceding the median class
• f = frequency of the median class
• h = form size

Way = \(l + [\dfrac {f_m-f_1}{2f_m-f_1-f_2}]\times h\)

where,

• l = lower limit of modal class,
• f_m= frequency of modal class,
• f_ane= frequency of class preceding modal grade,
• f₂= frequency of grade succeeding modal grade,
• h = class width

How to Find Mean Median and Style?

The hateful, median, and style for a given set of data tin be obtained using the hateful, median, formula. Click here to check these formulas in particular and sympathise their applications.

What Does Mean, Fashion, and Median Stand for?

Hateful, mode, and median are the three measures of central tendency in statistics. Mean represents the average value of the given set of data, while the median is the value of the middlemost observation obtained after arranging the data in ascending or descending order. Way represents the most common value. It tells you which value has occurred almost often in the given information. On a bar chart, the style is the highest bar. It is used with categorial data such every bit virtually sold T-shirts size.

How to Find Median Using Mean Median Fashion Formula?

Median is the value of the middlemost observation, obtained after arranging the data in ascending order.

To find the aforementioned, we need to consider two cases.

If n is odd, then apply the formula: Median = (north + 1)/2th observation.

If north is even, then utilize the formula: Median = [(n/2)thursday obs.+ ((northward/2) + 1)th obs.]/2

For grouped data, the median is obtained using the median formula:

Median = \(l + [\dfrac {\dfrac{n}{2}-c}{f}]\times h\)

Are Hateful, Mode, and Median the Aforementioned?

No, mean, way and median are non the same.

• Mean is the boilerplate of the given sets of numbers. Nosotros need to add the numbers upwardly so separate their sum by the number of observations.
• For finding the mode, we notice whether whatever number appears more than than once. The number which appears most is the mode. If there are other numbers that echo to the same level, there may be more than 1 mode. A set could be bimodal or trimodal. Simply the hateful of a given data is unique.
• Median is the value of the middlemost observation, obtained after arranging the data in ascending society.

Source: https://www.cuemath.com/data/mean-median-mode/

Posted by: westwelition.blogspot.com

Share this post